Research Areas
|
|
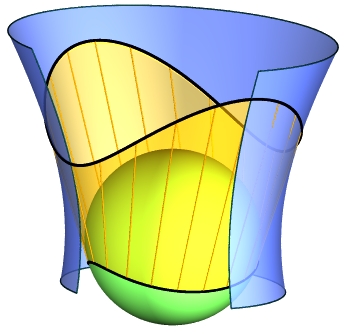Ruled surfaces, congruences of lines, and special complexes of lines have many applications
in kinematics and constructive geometry.
Line geometry is a natural higher-dimensional non-Euclidean geometry.
|
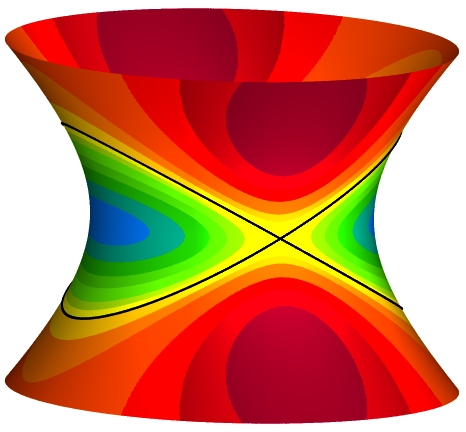Classical differential geometry deals with surfaces and curves in three-space and their
properties which can be described with the help of differential calculus.
Curvatures and curvature distributions on surfaces help to describe them.
|
|
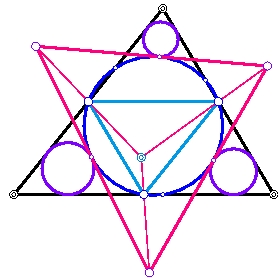The triangle is one of the simplest object in geometry.
There are still many open questions concerning the triangle in Euclidean as well as non-Euclidean planes.
Algebraic methods in combination with synthetic techniques are the most powerful tools in this area.
|
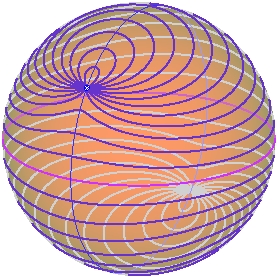Generalizations of well-known Euclidean constructions to arbitrary geometries lead to new classes of curves.
Some questions from geometric optics also result in new types of curves.
|
|
Point models of various geometries allow us to treat complicated geometric objects as points.
This simplification needs higher-dimensional model spaces and have a lot of applications.
|
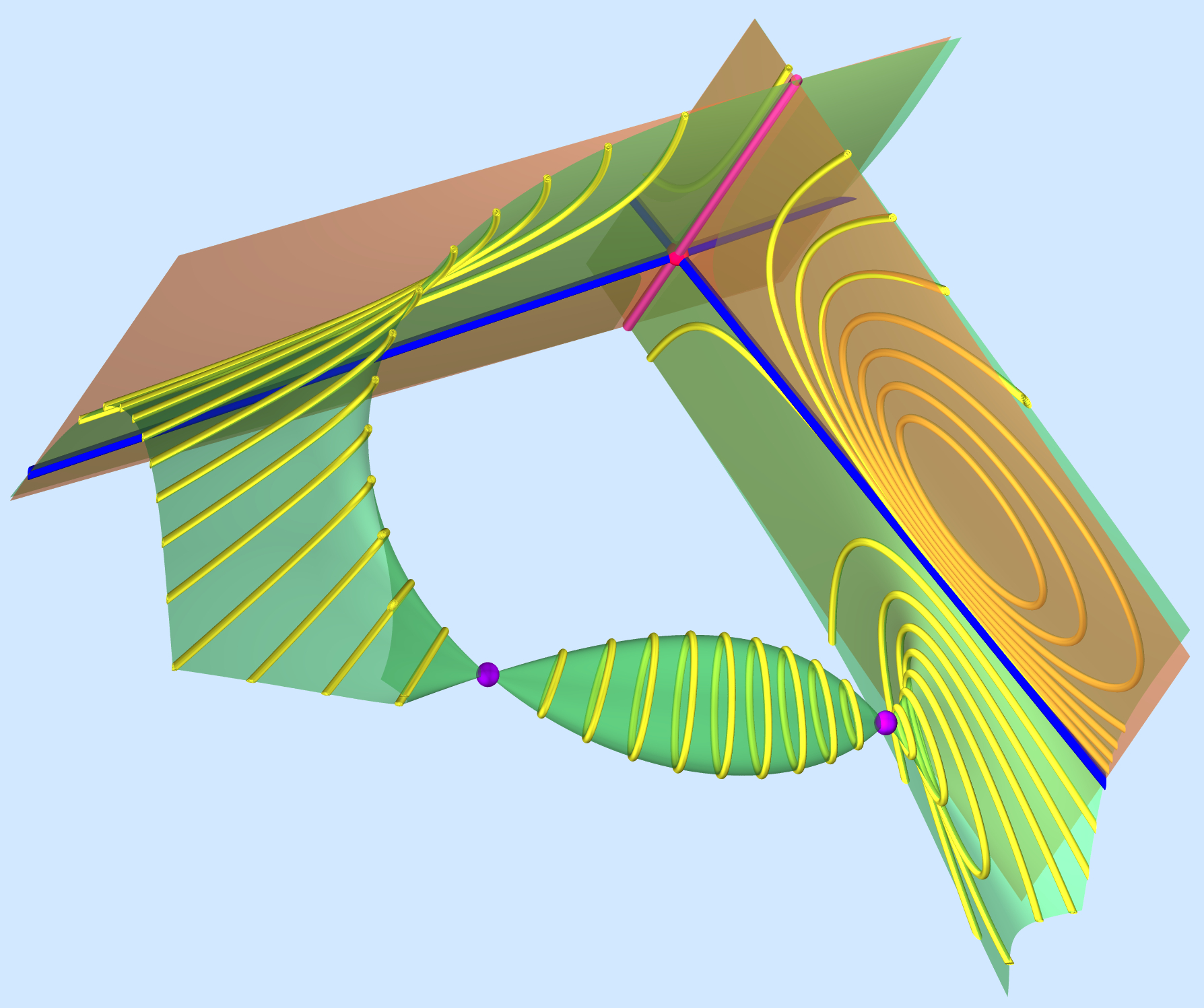Some surfaces arise in a natural way as set of points with certain properties.
We study singularities, metric, differential, and projective properties.
|
|
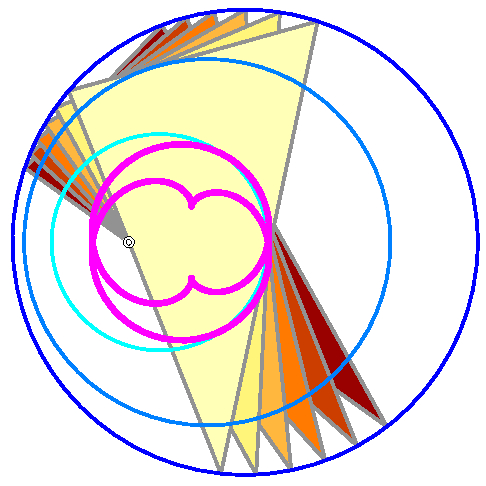Poncelet porisms of various forms bear a lot of algebraic problems.
Many phenomena can easily be observed with dynamic geometry software
and lead to a lot of conjectures, but
their verification needs a lot of tricky manipulations.
|
|