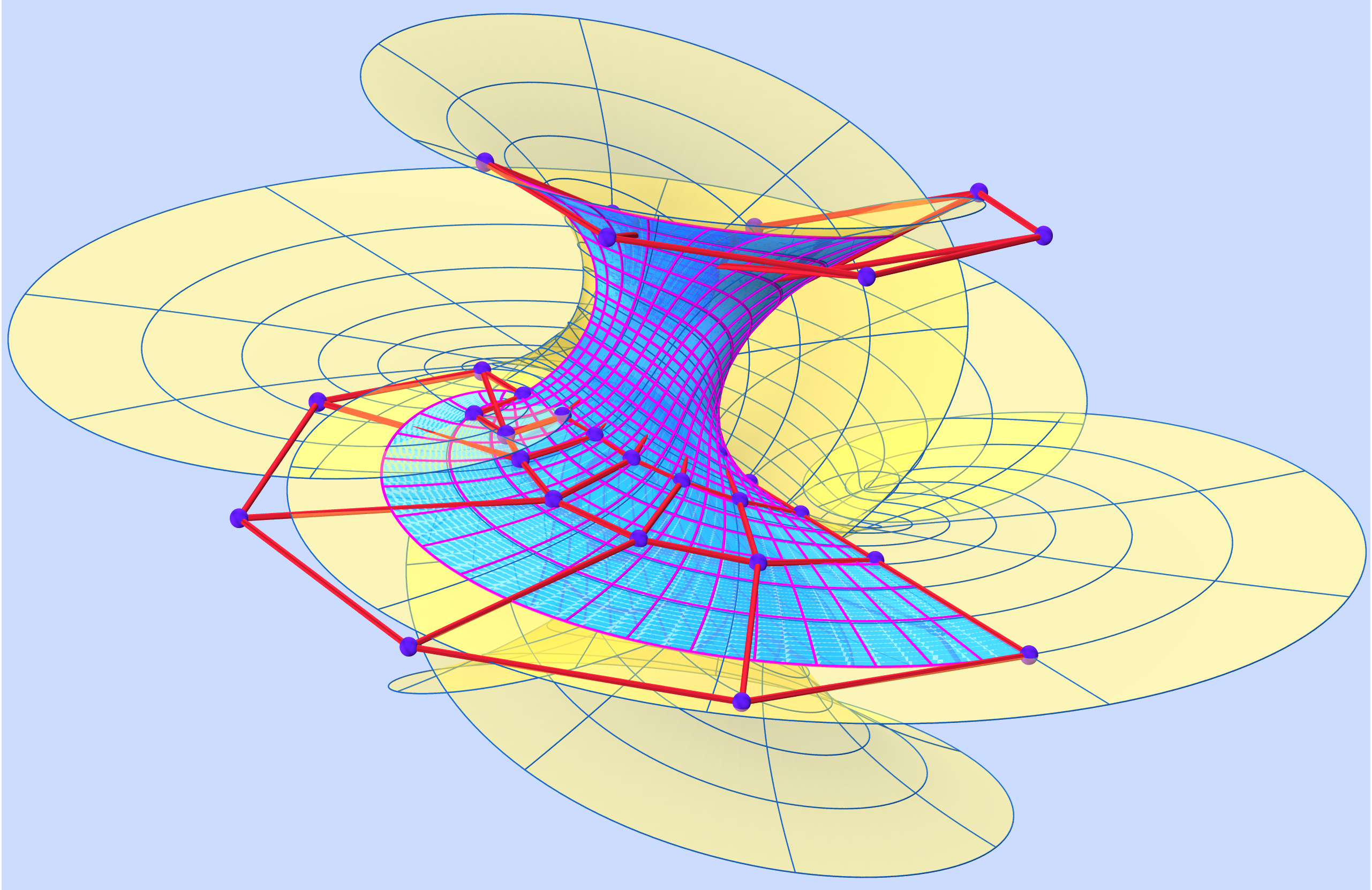
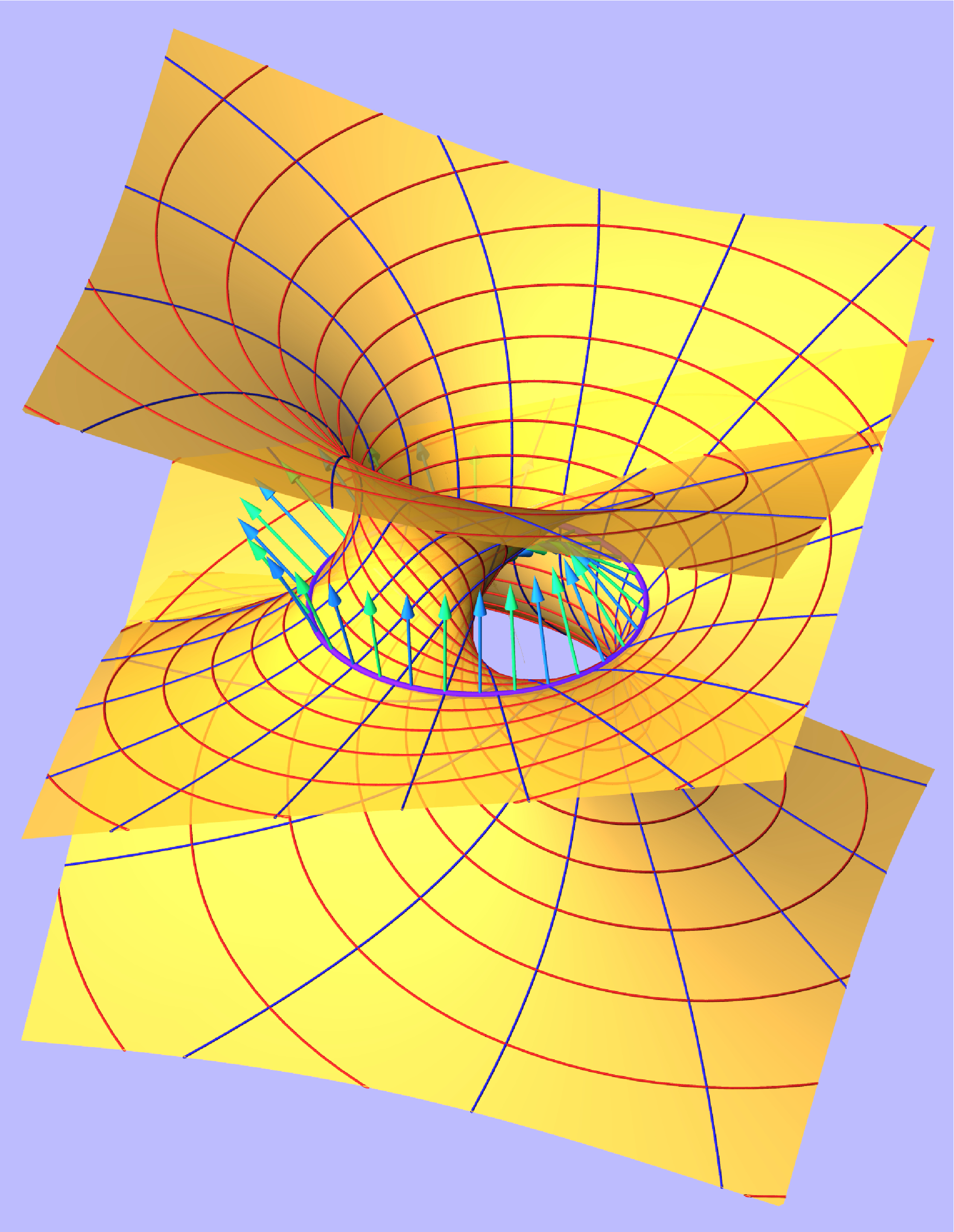
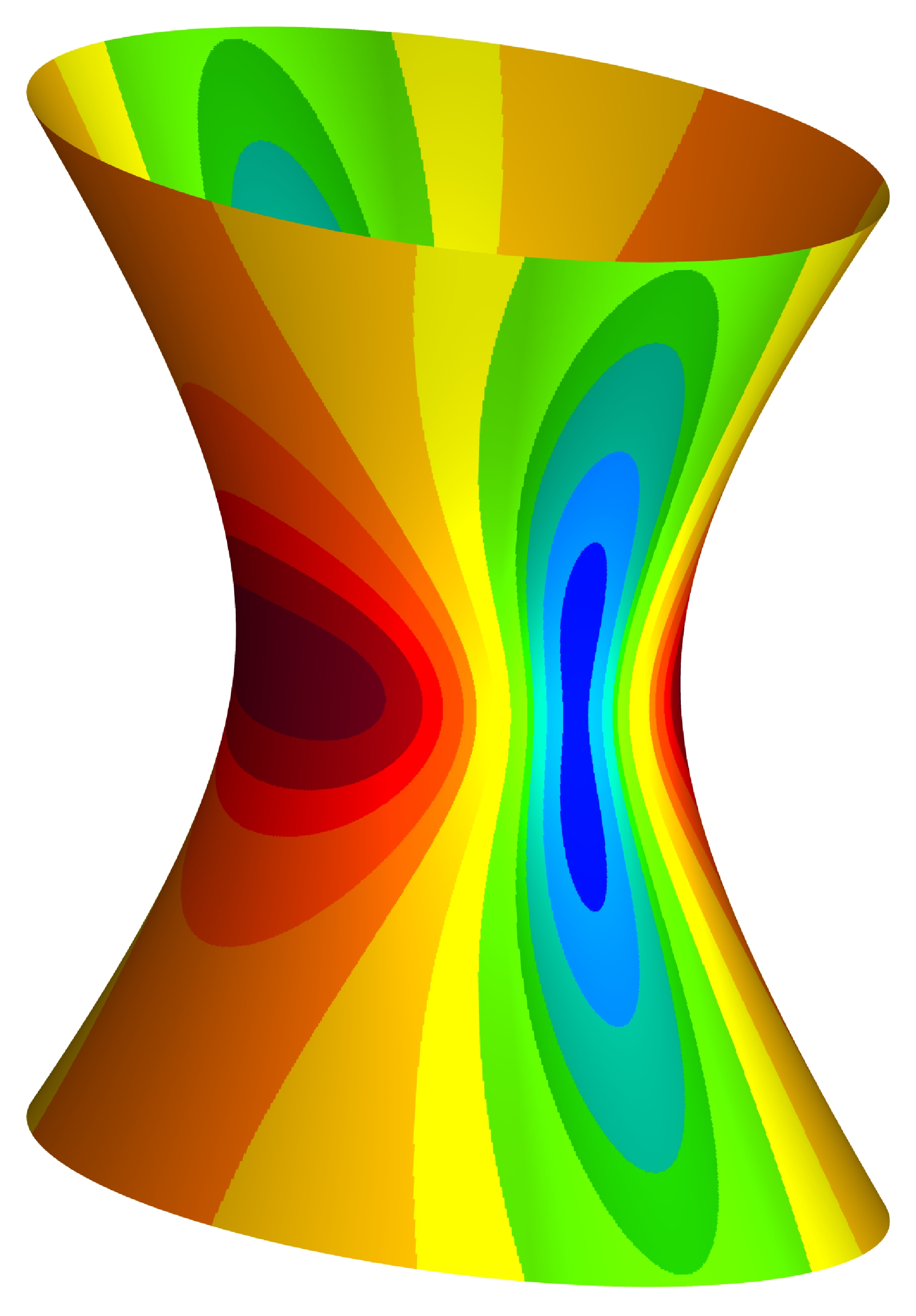
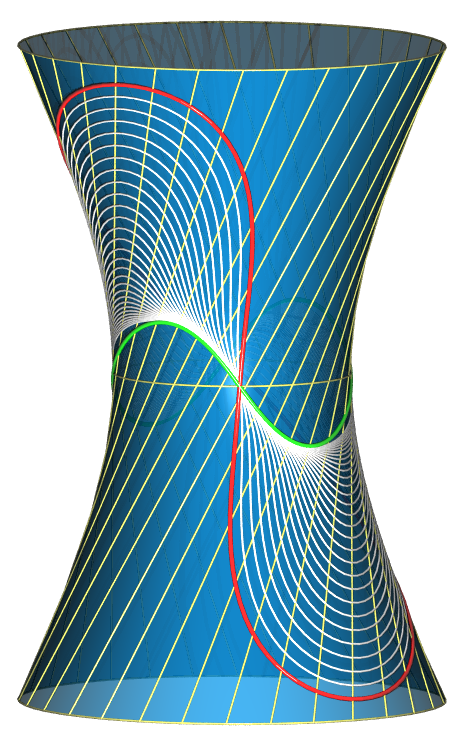
rational Bezier minimal surface with control structure
|
B. Odehnal.
On algebraic minimal surfaces. Although many results on algebraic minimal surfaces are known there are still some open questions. We pay our attention to algebraic minimal surfaces that admit even rational parametrizations since these can be given in the geometrically favorable Bezier representation. Especially some rational curves give rise to the construction of rationally parametrized minimal surfaces by solving the Björling problem. Curves of constant slope on quadrics of revolution are related to one-parameter families of rational minimal surfaces. Some low degree examples are given. |
a rational minimal Möbius strip
|
B. Odehnal.
A rational minimal Möbius strip. The simplest ruled surface of the topological type of a Möbius strip gives the boundary values for a minimal surface of genus one. Surprisingly, this minimal surface is algebraic and admits even rational parametrizations. The surface is of algebraic degree 11 and of class 15. Due to its construction, it carries rational cubics and closed harmonic oscillation curves. |
distribution of the Mean curvature on a one-sheeted hyperboloid
|
B. Odehnal.
Curvature functions on a one-sheeted hyperboloid. We study the distribution of some curvature functions on a one-sheeted hyperboloid by determining, describing, and visualizing the curves of constant Gaussian, Mean, principal curvature, and the curves of constant ratio of the principal curvatures. Our aim is a precise description of the regions of prescribed curvature values. It turns out that all these curves are algebraic and can be given in terms of implicit equations. Surprisingly, it is possible to derive an explicit parametrization of the curves of constant principal curvature in terms of algebraic functions. |
smoothing a discrete ruled surface |
M. Hagemann, D. Klawitter, and B. Odehnal: Curve flows on ruled surfaces. We study special flows of curves on ruled surfaces. Closed curves on closed ruled surfaces are driven by the Gaussian curvature flow and the geodesic curvature flow. For that we use a discretization of the ruled surfaces, the curves on them, and the curvatures. In an experimental part, the problem will be attacked numerically and various types of approximations will be used. |
convolution surface of two quadratic triangluar Bezier surfaces |
M. Peternell and B. Odehnal. Convolution surfaces of quadratic triangular Bézier surfaces. Comp. Aided Geom. Design 25 (2008), 116-129. We prove that the polynomial quadratic triangular Bezier surfaces are LN-surfaces. The reparametrization of the quadratic triangular Bezier surfaces is done in a way such that the normals obtain linear coordinate functions. The close relation to quadratic Cremona transformations is elucidated. These reparameterizations can be effectively used for the computation of convolution surfaces. |
Publications
|