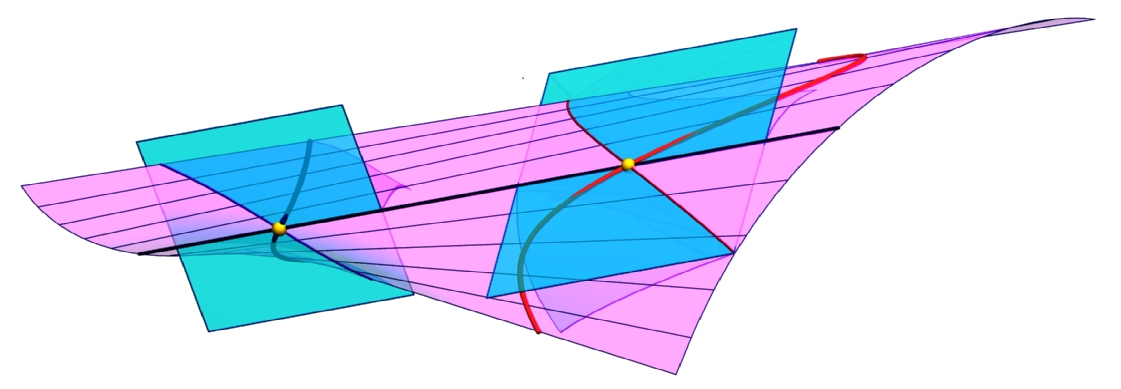
B. Odehnal: Note on flecnodes. J. Geom. Graphics 13/1 (2009), 29-40.

A flecnode F on a regular and non torsal ruling r of a ruled surface R is a point where R's asymptotic tangents along r hyperosculate the ruled surface. The name flecnode characterizes the intersection curve c of the tangent plane τ with R at F. It has a double point (a node) at F and this node is a point of inflection for both linear branches of c at F>. We show a way to parametrize the smooth one-parameter family of flecnodes of R which, in general, forms a curve with two branches. For that we derive the equation of the ruled quadric on three given lines in terms of Plücker coordinates of the given lines.

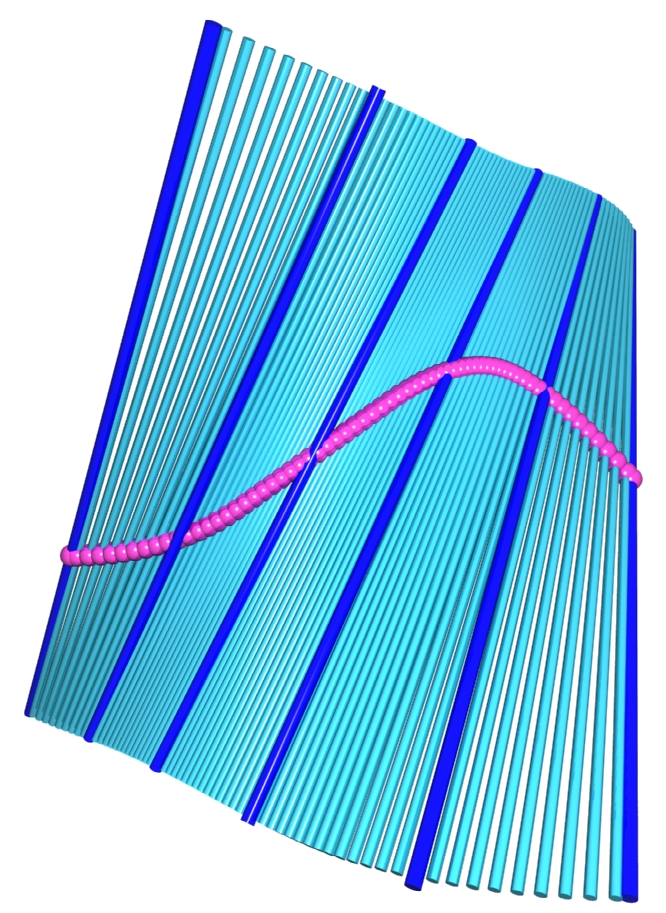
B. Odehnal: Subdivision algorithms for ruled surfaces.
J. Geom. Graphics 12/1 (2008), 35-52.

Recent research has produced results on subdivision in arbitrary manifolds. These results can be applied to the manifold of lines and thus we can create subdivision schemes especially for ruled surfaces. We present different methods for refining discrete models of ruled surfaces: An algorithm combining subdivision and projection to the manifold of lines in Euclidean three-space. A further algorithm combines subdivision for the striction curve with geodesic subdivision in the Euclidean unit sphere. The third method is based on the Denavit-Hartenberg method for serial robots. We refine the sequence of motions of the Sannia frame by means of geodesic subdivision in the group of Euclidean motions.

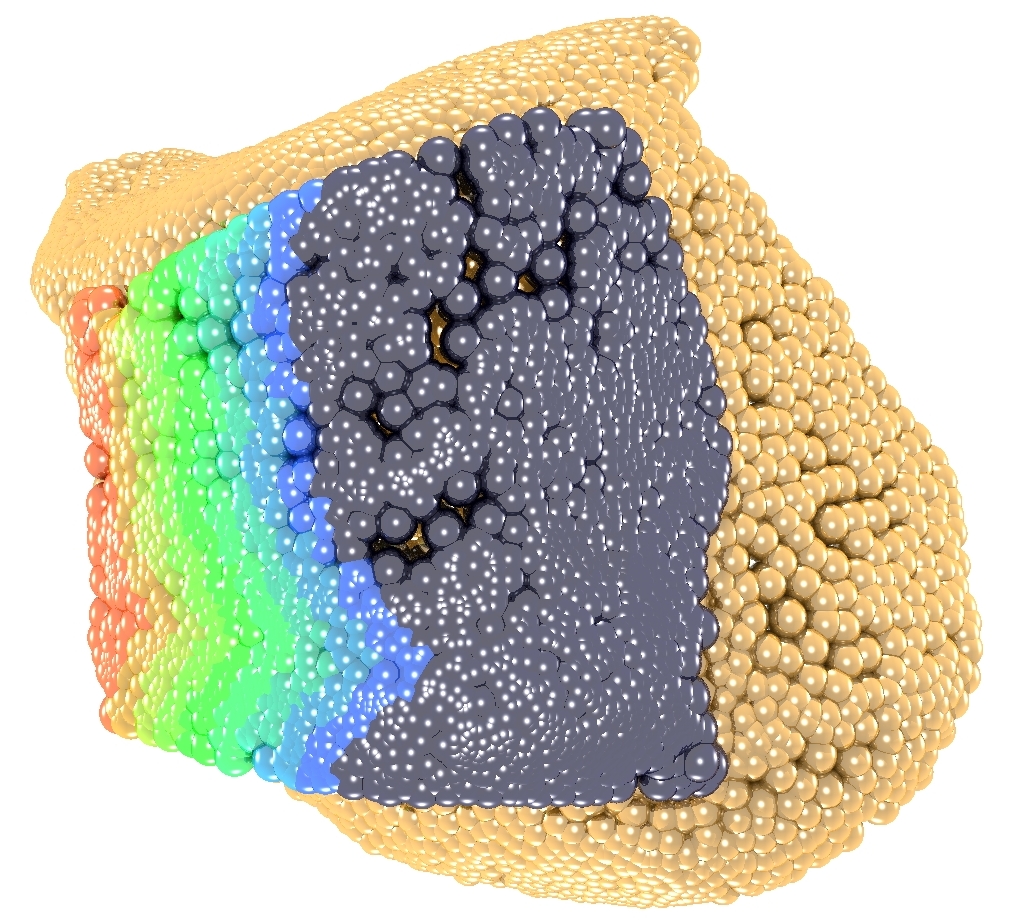
G.  Windisch, B. Odehnal, R. Reimann, F.  Anderhuber, and H. Stachel.
Contact areas of the tibiotalar joint.
Journal of Orthopedic Research 25/11 (2007), 1481-1487.

The contact areas between the articular surfaces of the talus and tibia are essential for understanding the mobility of the ankle joint. The purpose of our study was to reveal the contact area among the superior articular surface of the trochlea tali (target surface T) and the inferior articular surface of the tibia (query surface Q) under non-weight-bearing conditions in plantar flexion and dorsiflexion. Twenty cadaveric foot specimen were dissected and scanned by three-dimensional (3D) laser scanner to obtain data point sets. These point sets were triangulated and a registration procedure performed to avoid any intersection of the two joint surfaces. For all points of the query surface Q, the closest distance to T was measured. In 11 of 20 ankle joints, the contact area was larger in plantaflexion, in 5 it was nearly of equal size, and in 4 the two surfaces were found in a better congruence in dorsiflexion. The two articular surfaces can be in point or line contact and cause different motions while T is gliding on Q, so the original geometry of ligaments must be carefully reconstructed after injury or during total angle replacement. © 2007 Orthopedic Reasearch Society.

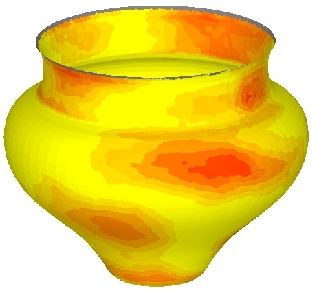
H. Pottmann, M. Hofer, B. Odehnal, and J. Wallner.
Line geometry for 3D shape understanding and reconstruction.
In T. Pajdla and J. Matas, editors, Computer Vision - ECCV 2004, Part I, volume 3021 of Lecture Notes in Computer Science, pages 297-309. Springer, 2004.

We understand and reconstruct special surfaces from 3D data with methods from line geometry. Based on estimated surface normals, we use approximation techniques in line space to recognise and reconstruct rotational, helical, developable, and other surfaces, which are characterised by the configuration of locally intersecting surface normals. For the computational solution we use a modified version of the Klein model of line space. Obvious applications of these methods lie in Reverse Engineering. We have tested our algorithms on real world data obtained from objects, such as antique pottery, gear wheels, and a surface of the ankle joint.