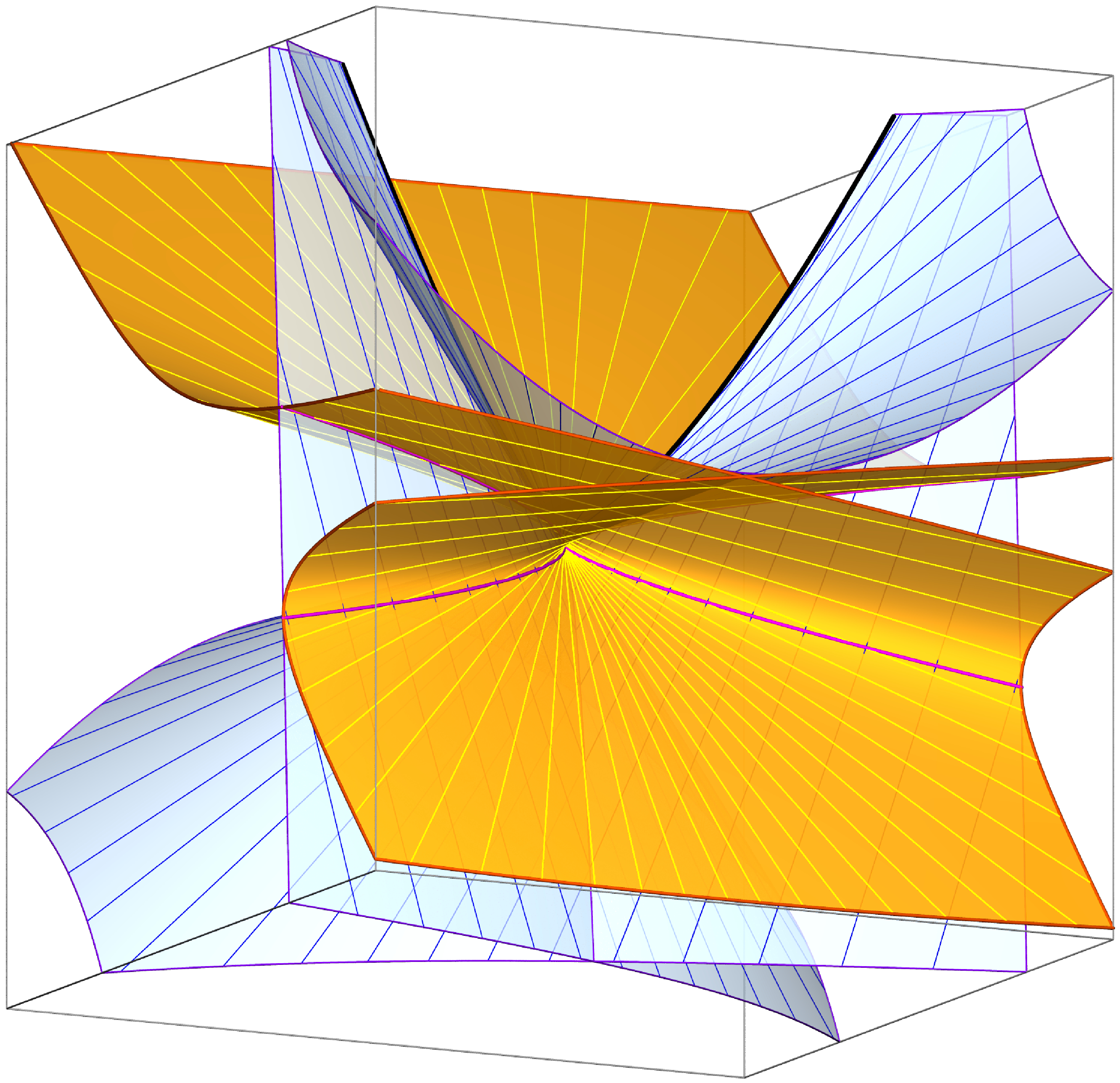
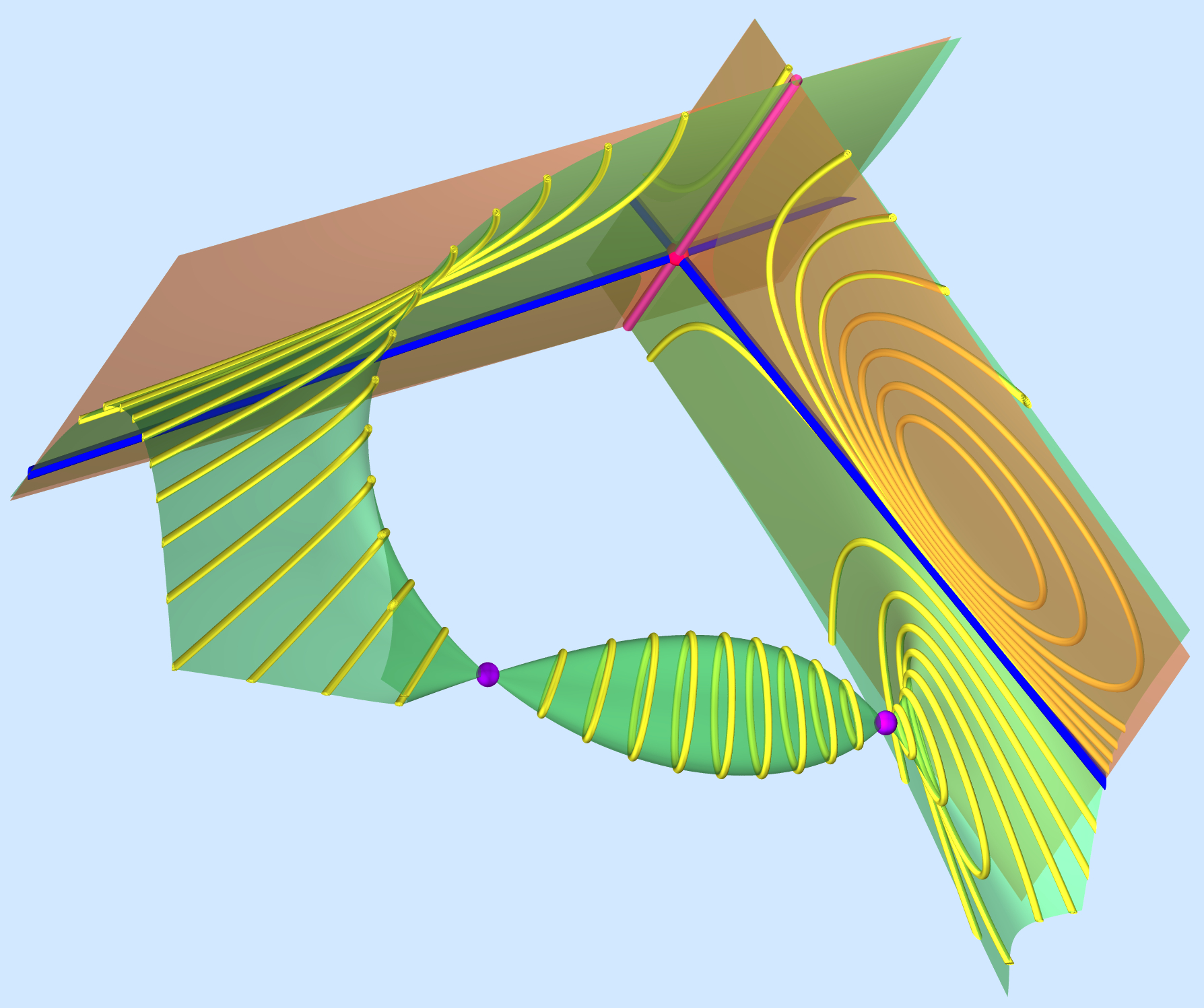
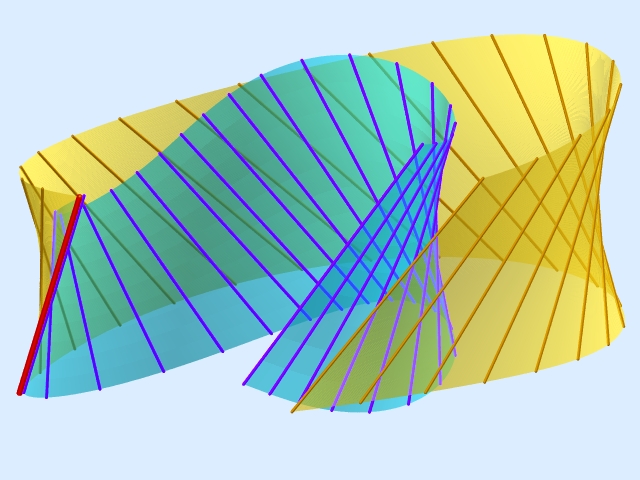
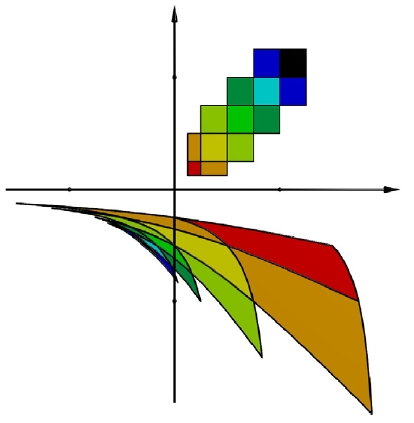
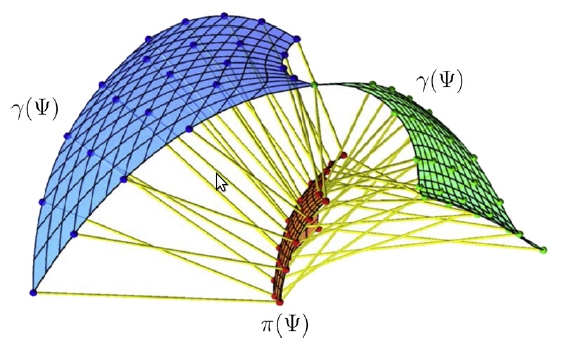
isoptic ruled surface of the tangent developable of a cusped quartic
|
B. Odehnal.
Isoptic ruled surfaces of developable surfaces. The notion of isoptics as is known from planar geometry cannot be carried over to three dimensions. One possible definition of isoptic surfaces can be given for developable ruled surfaces, since these are curves in the space of planes, i.e., the envelope of a one-parameter family of planes. Given a developable ruled surface R one can define the isoptic ruled surface J of R as the set of all intersection lines of pairs of tangent planes of R that enclose a fixed angle. The isoptic ruled surfaces of developable ruled surfaces that are either invariant under one-parameter subgroups of the group of Euclidean or equiform motions are helical or spiral ruled surfaces. Although the isoptics of cylinders and cones can be found in an elementary way, they fall into the class of invariant surfaces. Surprisingly, the orthoptic ruled surfaces of developables whose curves of regression admit a monoidal (polynomial) parametrization can be generated by means of a projective mapping acting on the curve of regression assigning to each point (and its osculating plane) precisely that point with the orthogonal osculating plane. These orthoptic always fall into a certain number of separate branches. |
isometric rational minimal surfaces on curves of constant slope
|
Although many results on algebraic minimal surfaces are known there are still some open questions. We pay our attention to algebraic minimal surfaces that admit even rational parametrizations since these can be given in the geometrically favorable Bezier representation. Especially, some rational curves give rise to the construction of rationally parametrized minimal surfaces by solving the Björling problem. Curves of constant slope on quadrics of revolution are related to one-parameter families of rational minimal surfaces. Some low degree examples are given. |
cubic surface of pivot points with coplanar pedal points
|
The Wallace-Simson-Theorem in the plane states that the three pedal points on the side line of a triangle are collinear if the pivot point is chosen on the circumcircle of the triangle. In the spatial version, we ask for pivot points such that four pedal points on the sides of a skew quadrilateral are coplanar. It turns out that the set of such pivot points forms a cubic surface whose four nodes coincide with the vertices of the skew quadrilateral. In this paper we look for conditions on the quadrilateral such that the cubic surface degenerates. For that purpose, we derice algebraic condidtions on the coefficients of a generic cubic surface such that a linear polynomial splits of. We can classify the skew quadrilaterals with partly or completely degenerate cubic Simson surface. |
quartic surface of endpoints of segments from a point
with equally long central images
|
B. Odehnal. Distances and Central Projections. KoG 18 (2014), 28-35. Consider a central projection κ with center O from projectively extended Euclidean three-space onto some plane π. The set of all endpoints Q of line segments PQ starting at a certain point P with equally long central images, i.e., dist(P,Q)=dist(κ(P),κ(Q)) form a quartic surface with two conical nodes and a double line at infinity. The quartic surface carries a one-parameter family of circles, three real lines, and two pairs of isotropic lines. |
line geometric conchoid of a ruled surface
|
M. Hamann and B. Odehnal.
Conchoidal ruled surfaces. The planar construction of conchoids is translated to the Klein model of line geometry. In this setting conchoids of ruled surfaces are again ruled surfaces. Depending on the choice of focal lines we obtain either a collinear transform of the given ruled surface or a quadratic image, but stil a ruled surface. We study some low degree examples at hand of a special affine version of the projective conchoid transform. |
action of a Cremona transformation applied to pattern of squares
|
M. Peternell and B. Odehnal. In the present paper we prove that the polynomial quadratic triangular Bézier surfaces are LN-surfaces. We demonstrate how to reparameterize the surfaces such that the normals obtain linear coordinate functions. The close relation to quadratic Cremona transformations is elucidated. These reparameterizations can be effectively used for the computation of convolution surfaces. |
rational envelope of a two-parameter family of spheres |
M. Peternell and B. Odehnal, and L.M. Sampoli. We investigate rational two-parameter families of spheres in Euclidean three-space and give sufficient conditions for the rationality of their envelope. The four-dimensional cyclographic model of the set of spheres in Euclidean three-space is an appropriate framework to show that quadratic Bezier patches in a four-dimensional (pseudo-Euclidean) space lead to a two-parameter family of spheres with rational envelope surfaces. Moreover, this construction can be generalized to obtain a larger class of surfaces sharing the property of rational envelopes. |
Publications
|