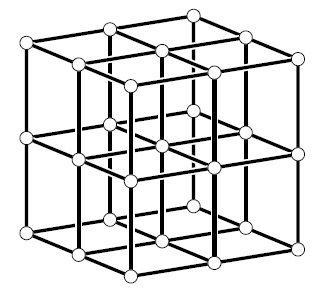
a linear image of the Segre variety S1,1,1(2)
|
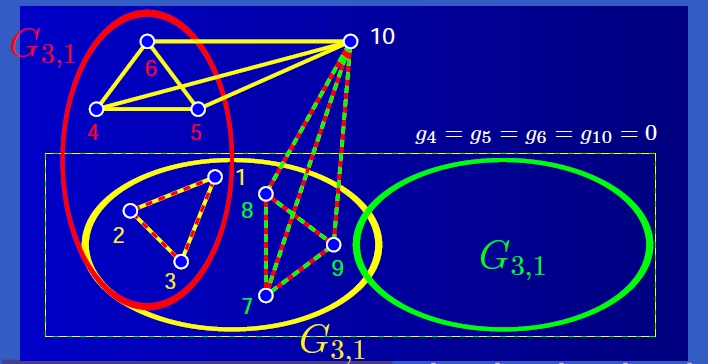
H. Havlicek,B. Odehnal, and M. Saniga. On invariant notions of Segre varieties in binary projective spaces. Des. Codes Cryptogr. 62 (2012), 343-356. Invariant notions of a class of Segre varieties S(m) of PG(2m-1,2) that are direct products of m copies of PG(1,2), m being any positive integer, are established and studied. We first demonstrate that there exists a hyperbolic quadric that contains S(m) and is invariant under its projective stabiliser group Stabm(2). By embedding PG(2m-1,2) into PG(2m-1,4), a basis of the latter space is constructed that is invariant under Stabm(2) as well. Such a basis can be split into two subsets of an odd and even parity whose spans are either real or complex-conjugate subspaces according as m is even or odd. In the latter case, these spans can, in addition, be viewed as indicator sets of a Stabm(2)-invariant geometric spread of lines of PG(2m-1,2). This spread is also related with a Stabm(2)-invariant non-singular Hermitian variety. The case m= is examined in detail to illustrate the theory. Here, the lines of the invariant spread are found to fall into four distinct orbits under Stab3(2), while the points of PG(7,2) form five orbits. |
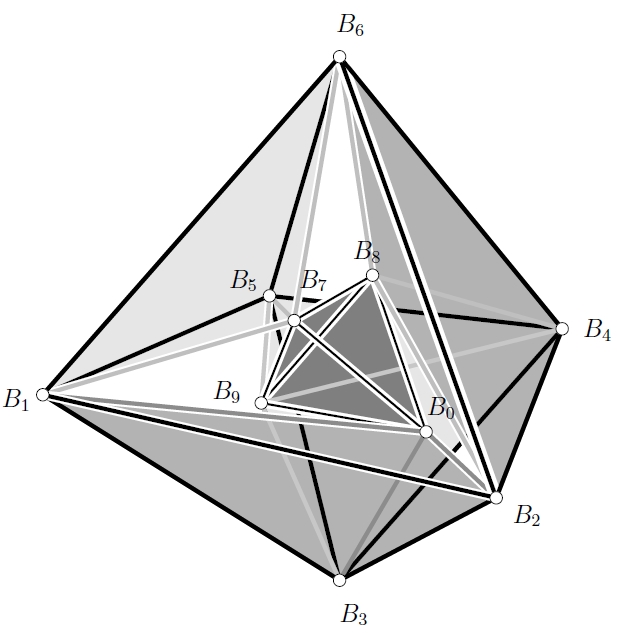
vertices of cones in a twentythree-dimensional space
|
B. Odehnal. Die Linienelemente des P3. Österreich. Akad. Wiss. Math.-Naturw. Kl. S.-B. II 215 (2006) 155-171.
Die vorliegende Arbeit befaßt sich mit der Abbildung der Linienelemente des dreidimensionalen
projektiven Raumes P3 auf die Punkte einer fünfdimensionalen rationalen Fläche
M5, die in den neundimensionalen projektiven Raum P9 eingebettet ist.
Ferner wird der Zusammenhang zwischen der Segre-Varietät S3,5 und der Mannigfaltigkeit
M5 untersucht. Auf der Modellfläche erscheinen einfache Linienelementmannigfaltigkeiten
als projektive Unterräume wieder. Das Dualitätsprinzip der projektiven Geometrie gestattet die
Übertragung der Ergebnisse über Linienelemente auf ihre dualen Gegenstücke. |
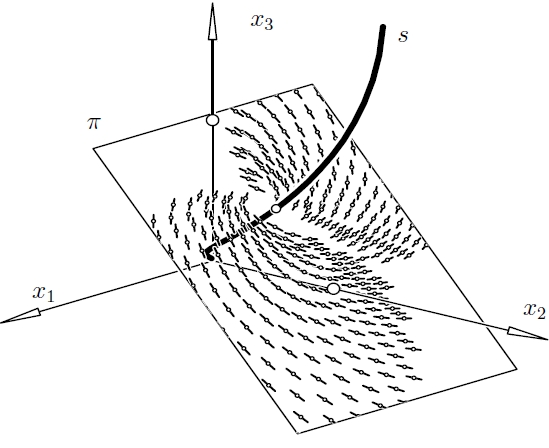
line elements of a linear complex of line elements within a plane
|
B. Odehnal, H. Pottmann, and J. Wallner. Equiform kinematics and the geometry of line elements. Beitr. Algebra Geom. 47/2 (2006), 567-582. The geometry of lines is a classical topic which is of interest not only for its own sake. Given the nature of its object of study, the lines of Euclidean or projective three-space, it is natural that frequently problems on the borderlines between mathematics, computer science, and engineering are solved with line-geometric methods. The number of applications where lines and points on them (i.e., line elements) appear together raises interest in the geometry of line elements. This paper generalizes the concept of Plücker coordinates to the case of line elements and establishes some basic facts. We emphasize the relation with equiform kinematics, thus generalizing the well known relations between Euclidean kinematics and classical line geometry. |
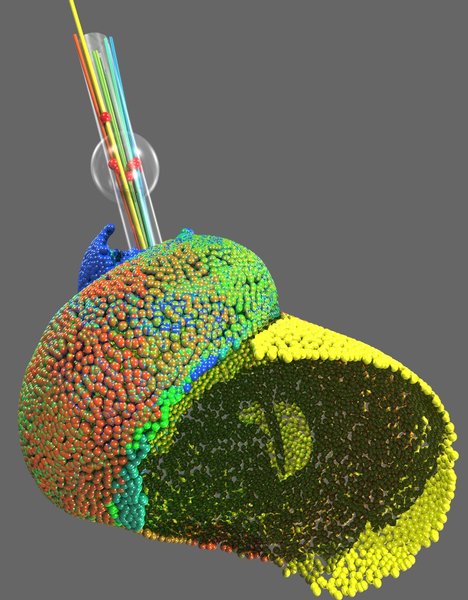
reconstruction of spiral axis+ center for randomly chosen parts of a shell of
Turbo marmoratus
|
B. Odehnal, H. Pottmann, and J. Wallner. Equiform kinematics and the geometry of line elements. Beitr. Algebra Geom. 47/2 (2006), 567-582. This paper presents a new method for the recognition and reconstruction of surfaces from 3D data. Line element geometry, which generalizes both line geometry and the Laguerre geometry of oriented planes, enables us to recognize a wide class of surfaces (spiral surfaces, cones, helical surfaces, rotational surfaces, cylinders, etc.) by fitting linear subspaces in an appropriate seven-dimensional image space. In combination with standard techniques such as PCA and RANSAC, line element geometry is employed to effectively perform the segmentation of complex objects according to surface type. Examples show applications in reverse engineering of CAD models and testing mathematical hypotheses concerning the exponential growth of sea shells. |
configuration of vertices of the quadratic cones through the flag manifold
|
B. Odehnal. Flags in Euclidean three-space. Math. Pannon. 17/1 (2006), 29-48. This paper is devoted to the study of flags in Euclidean three-space. Coordinates of flags are defined and a point model in a projective space is discussed. It turns out that the six-dimensional manifold of flags in Euclidean three-space can be embedded into a nine-dimensional projective space. There this manifold is a delPezzo surface of degree five and thus it allows a rational parametrization. The group of Euclidean motions acting transitively on the flags in Euclidean three-space induces a subgroup of automorphic collineations of the model surface. We study special subsets of the manifold of flags and show the close relations to Euclidean kinematics and Non-Euclidean geometries. |
Publications
|