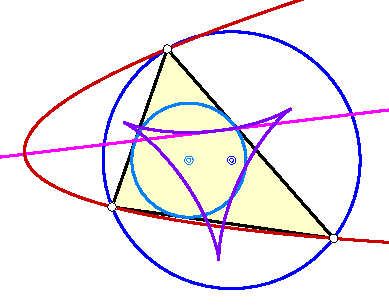
The axis of the circumparabolas for all triangles in the poristic
family envelop a Steiner cycloid. |
B. Odehnal, D. Reznik.
Circumparabolas in Chapple's porism. The circumparabolas of the one-parameter family of triangles in Chapple's porism constitute a two-parameter family of parabolas each of which corresponding to the points of a quadratic cone in the Veronese manifold. The axes of the circumparabolas for each fixed triangle envelop a Steiner cycloid. We rediscover the circumparabola-vertex-septic and the circumparabola-focus-quintic which house the vertices and foci of the circumparabolas of three points independent of whether they are related to porisms or not. The axis of circumparabolas with fixed pivot on the circumcircle are concurrent. The envelope of all Steiner cycloids consist of two ellipses, one containing the cycloids' cusps, the other one touching the cycloids from the interior. |
The incenter and the excenters may change their roles over
the course of a poristic turn. |
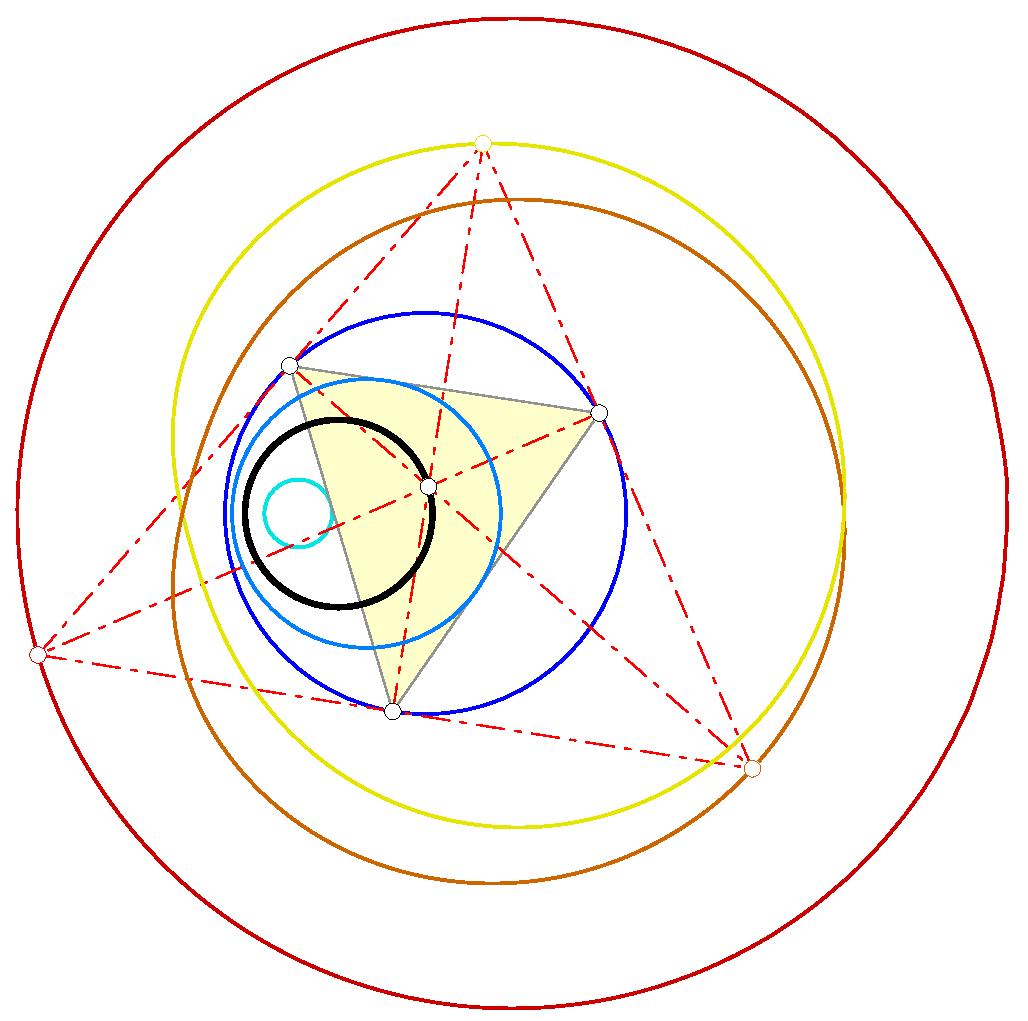
R.A. Garcia, B. Odehnal, D. Reznik. Loci of Poncelet Triangles in the General Closure Case. J. Geom 113:17 (2022), 30 pages.
We study the traces of triangle centers in various types of Poncelet porisms.
Giving up the uniqueness of the incircle of the triangles of a poristic family,
we observe that the paths of the excenters spread into several components.
However, there are centers whose poristic traces are still conics. |
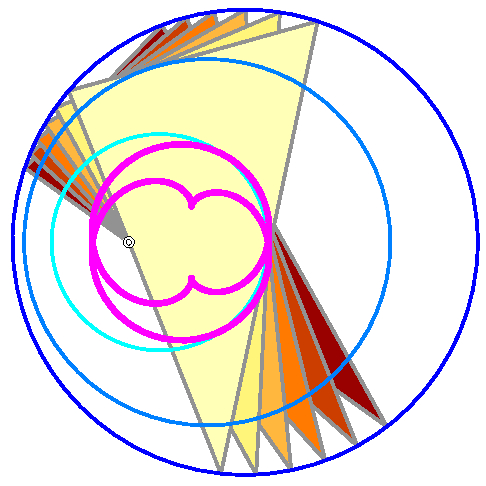
Circular orbits spread into several components once the
incircle is not the unique support. |
R.A. Garcia, B. Odehnal, D. Reznik. Poncelet porisms in hyperbolic pencils of circles. J. Geom. Graphics 25/2 (2021), 205-225. Poncelet porisms cover Chapple's porism (triangles with common incircle and circumcircle) as a special case. The most general form of Poncelet porism deals with polygons interscribed between conics of a pencil. The circles of a hyperbolic pencil of circle can also serve as the support of poristic families of polygons. The radii, or equivalently, the central distances of the circles have to fulfill some algebraic conditions in order to allow for interscribed polygons. We also observe opportunistic polygons which show up as additional solutions to the high algebraic degree of the closure conditions and the fact that from each point we can draw two tangents to a conic. |
Chapple's porism causes many circular orbits. |
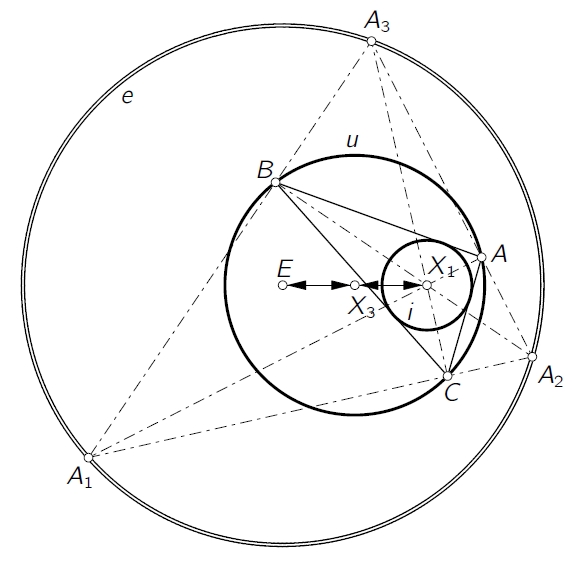
B. Odehnal: Poristic loci of triangle centers. J. Geom. Graphics 15/1 (2011), 45-67. The one-parameter family of triangles with common incircle and circumcircle is called a porisitic system of triangles. The triangles of a poristic system can be rotated freely about the common incircle. However, this motion is not a rigid body motion for the side lengths of the triangle are changing. Surprisingly many triangle centers associated with the triangles of the poristic family trace circles while the triangle traverses the poristic family. Other points move on conic sections, some points trace more complicated curves. We shall describe the orbits of centers and some other points. Thereby we are able to answer open questions and verify some older results. |
Publications
|