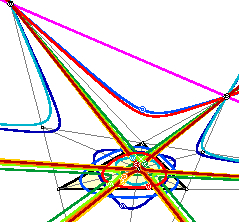
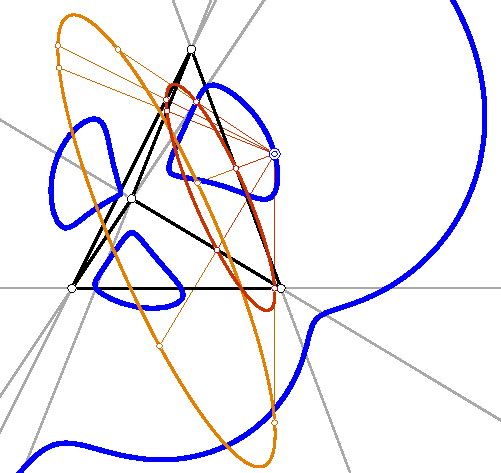
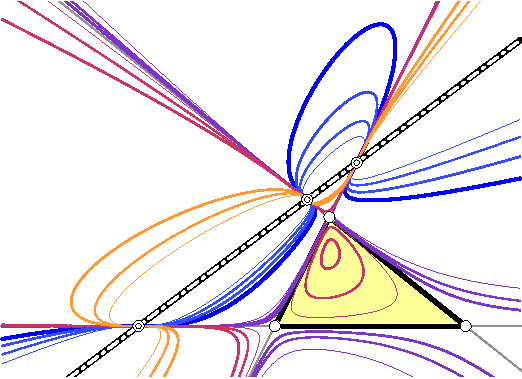
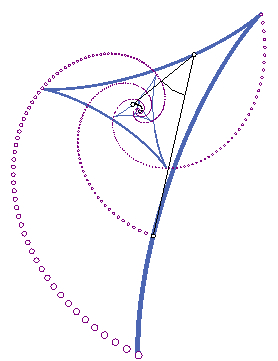
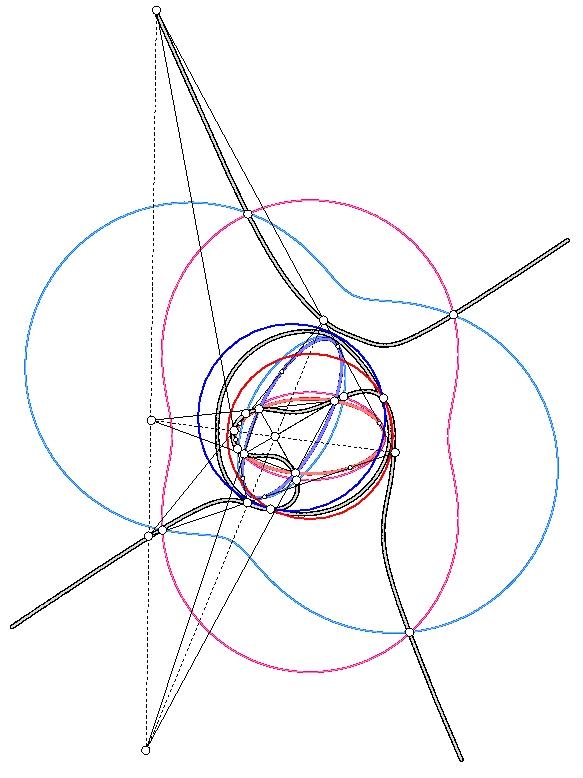
permutation cubics
| B. Odehnal. Permutation cubics. In: ICGG 2022 - Proceedings of the 20th International Conference on Geometry and Graphics. L.-Y. Cheng (ed.) Lecture Notes on Data Engineering and Communications Technologies vol. 146, ISBN 978-3-031-13587-3 paper no. 005, 59-70. Permuting the trilinear coordinates of a point P yields six (permutation) points that lie on a single conic which is called the permutation conic. The six permutation points of P and the six permutation points of the isogonal or isotomic conjugate of P lie on a cubic curve which shall be called the permutation cubic associated with P. To each point in the triangle plane we can assign a permutation cubic and some centers share their permutation cubic. Among the many possible permutation cubics only a few rational ones are known and some hundred triangle centers define a degenerate triangle cubic. |
the septic locus of points with conconic pedal points
| B. Odehnal. A rarity in geometry: a septic curve. KoG 25/25 (2021), 25-39.
Septic curves play a rather marginal role in geometry.
This is due to the fact that the distance and angle metrics usually involve
qudratic functions.
The algebraic formulation of geometric problems involving distances and angles
normally results in qudratic, quartic, octic, ... equations and curves of the
like degree.
Curves of odd degrees come along if, eg., linear components split off from an
equation. |
projective view on the pencil of distance product cubics
| B. Odehnal. Distance Product Cubics. KoG 24/24 (2020), 29-40. Given a triangle in the Euclidean plane, one can ask for the set k of all points that form a constant product of distances to the side lines of the triangle. It turns out that k is an elliptic cubic curve except in one case. The exceptional case occurs for those points that share the distance product with the centroid of the base triangle. The centroid is the isolated node on this particular cubic which is the only known cubic, called Bataille acnodal cubic. The totality of all these distance product cubics forms a pencil of cubics including the two degenerate cubics: the union of the triangle's side lines and the three-fold line at infinity. All cubics share the three real points of inflection which are the three common real ideal points. The comparison of the distance products of triangle centers from Kimberling's list shows that only a small number of centers share their distance product cubics with other centers. |
example of an autoisoptic curve of
| B. Odehnal. Examples of autoisoptic curves. Proc. 17thIntern. Conf. Geometry and Graphics, Aug. 3-7, 2018, Milan/Italy, article No. 082, 350-361. The isoptic curve of a planar curve is the locus of all points where tangents of the curve meet at a certain fixed angle. We describe curves in the Euclidean plane that agree with their isoptic curves. Representing a curve by its support function enables us to give conditions on the support function of an autoisoptic curve. These conditions turn out to be a pair of ordinary delay differential equations imposed on a single support function. Therefore, the generic case can only be handled by means of approximations in function space. Some special cases occur under certain circumstances: This delivers the well-known autoevolutes by W. Wunderlich. Further, we also obtain autoevolutoides as generalization of Wunderlich's curves which are also examples of autoisoptic curves. We give some examples of autoisoptic curves and provide some approximate solutions of the system of ordinary delay differential equations. |
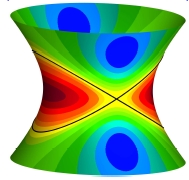
isolines of the Mean curvature on a one-sheeted hyperboloid
|
B. Odehnal. Curvature functions on a one-sheeted hyperboloid. Proc. 16th Intern. Conf. Geometry and Graphics, Aug. 4-8, 2014, Innsbruck/Austria, article No. 076. We study the distribution of some curvature functions on a one-sheeted hyperboloid by determining, describing, and visualizing the curves of constant Gaussian, Mean, principal curvature, and the curves of constant ratio of the principal curvatures. Our aim is a precise description of the regions of prescribed curvature values. It turns out that all these curves are algebraic and can be given in terms of implicit equations. Surprisingly, it is possible to derive an explicit parametrization of the curves of constant principal curvature in terms of algebraic functions. |
A spherical conchoid is the intersection of the sphere and a quartic surface.
|
B. Odehnal. Conchoids on the sphere. KoG 17 (2014), 43-52. The construction of planar conchoids can be carried over to the Euclidean unit sphere. We study the case of conchoids of (spherical) lines and circles. Some elementary constructions of tangents and osculating circles are stil valid on the sphere. Further, we aim at the illustration and a precise description of the algebraic properties of the principal views of spherical conchoids, i.e., the conchoid's images under orthogonal projections onto their symmetry planes. |
equioptic curve of a pair of conics computed from the respective sets of isoptic curves |
B. Odehnal.
Equioptic curves of conic sections. Given two plane curves c1 and c2 we call the set of points from which c1 and c2 are seen under equal angle the equioptic curve. We give some basic results concerning equioptic curves in general. Then we pay our attention to the seemingly simple case of equioptic curves of conic sections. Mainly we are interested in upper bounds of the algebraic degree of these curves. Some examples illustrate the results. We pay our attention to some special configurations of conic sections, such as touching or osculating conics and confocal conics. |
Publications
|