Steiner Miquel transformation acdting on
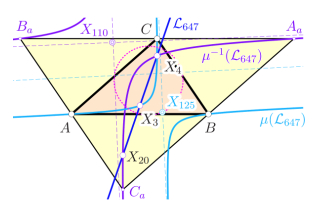
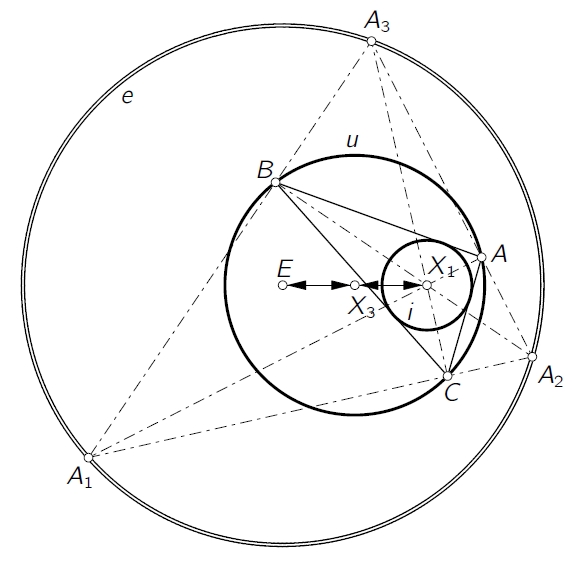
| B. Odehnal. A Miquel-Steiner Transformation. KoG 27/27 (2023), 14-24. Each complete quadrilateral has three Miquel-Steiner points. Any triangle together with an arbitrarily chosen point not on a triangle side also defines a complete quadrilateral, and thus, this pivot point defines three Miquel-Steiner points. These three Miquel points form a triangle which is perspective with the base triangle. The mapping that assigns to the pivot point the uniquely defined perspector is a quadratic and not involutive Cremona transformation and shall be called Miquel-Steiner transformation. We shall study the action of the Miquel-Steiner transformation and its inverse applied to some lines and circles related to the triangle. |
permutation cubics
| B. Odehnal. Permutation cubics. In: ICGG 2022 - Proceedings of the 20th International Conference on Geometry and Graphics. L.-Y. Cheng (ed.) Lecture Notes on Data Engineering and Communications Technologies vol. 146, ISBN 978-3-031-13587-3 paper no. 005, 59-70. Permuting the trilinear coordinates of a point P yields six (permutation) points that lie on a single conic which is called the permutation conic. The six permutation points of P and the six permutation points of the isogonal or isotomic conjugate of P lie on a cubic curve which shall be called the permutation cubic associated with P. To each point in the triangle plane we can assign a permutation cubic and some centers share their permutation cubic. Among the many possible permutation cubics only a few rational ones are known and some hundred triangle centers define a degenerate triangle cubic. |
projective view on the pencil of distance product cubics
| B. Odehnal. Distance Product Cubics. KoG 24/24 (2020), 29-40. Given a triangle in the Euclidean plane, one can ask for the set k of all points that form a constant product of distances to the side lines of the triangle. It turns out that k is an elliptic cubic curve except in one case. The exceptional case occurs for those points that share the distance product with the centroid of the base triangle. The centroid is the isolated node on this particular cubic which is the only known cubic, called Bataille acnodal cubic. The totality of all these distance product cubics forms a pencil of cubics including the two degenerate cubics: the union of the triangle's side lines and the three-fold line at infinity. All cubics share the three real points of inflection which are the three common real ideal points. The comparison of the distance products of triangle centers from Kimberling's list shows that only a small number of centers share their distance product cubics with other centers. |
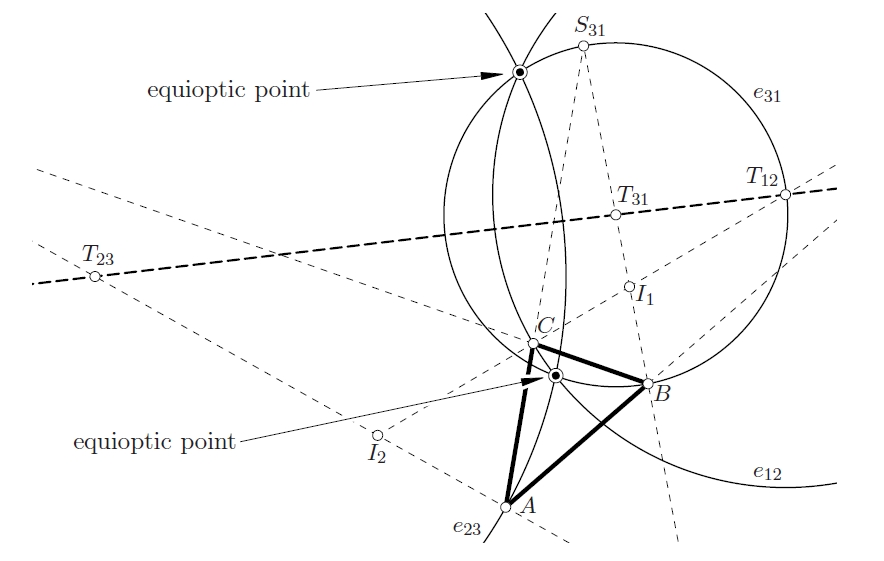
The sides of a triangle can be seen at equal angles from the equioptic points of the triangle.
|
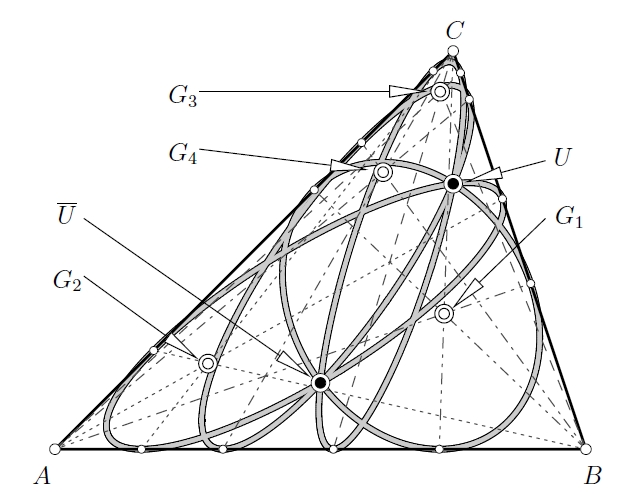
B. Odehnal: Equioptic points of a triangle. J. Geom. Graphics 17/1 (2013), 15-24. The locus of points where two non-concentric circles c1 and c2 are seen under equal angles is the equioptic circle e. The equioptic circles of the excircles of a triangle Δ have a common radical axis r. Therefore the excircles of a triangle share up to two real points, i.e., the equioptic points of Δ from which the circles can be seen under equal angles. The line r carries a lot of known triangle centers. Further we find that any triplet of circles tangent to the sides of Δ has up to two real equioptic points. The three radical axis of triplets of circles containing the incircle are concurrent in a new triangle center. |
Chapple's porism causes many circular orbits. |
B. Odehnal: Poristic loci of triangle centers. J. Geom. Graphics 15/1 (2011), 45-67. The one-parameter family of triangles with common incircle and circumcircle is called a porisitic system of triangles. The triangles of a poristic system can be rotated freely about the common incircle. However, this motion is not a rigid body motion for the sidelengths of the triangle are changing. Surprisingly many triangle centers associated with the triangles of the poristic family trace circles while the triangle traverses the poristic family. Other points move on conic sections, some points trace more complicated curves. We shall describe the orbits of centers and some other points. Thereby we are able to answer open questions and verify some older results. |
projective version of Gergonne and Nagel points |
B. Odehnal: Generalized Gergonne and Nagel points Beitr. Algebra Geom. 51/2 (2010), 477-491. We show that the Gergonne point G of a triangle Δ in the Euclidean plane can in fact be seen from a more general point of view, i.e., from the viewpoint of projective geometry. So it turns out that there are up to four Gergonne points associated with Δ. The Gergonne and Nagel point are isotomic conjugates of each other, and thus we find up to four Nagel points associated with a generic triangle. We reformulate the problems in a more general setting and illustrate the different appearances of Gergonne points in different affine geometries. Darboux's cubic can also be found in the more general setting, and finally a projective version of Feuerbach's circle appears. |
the first and second Odehnal point, see
Encyclopedia of Triangle Centers |
B. Odehnal.
Some triangle centers associated with the
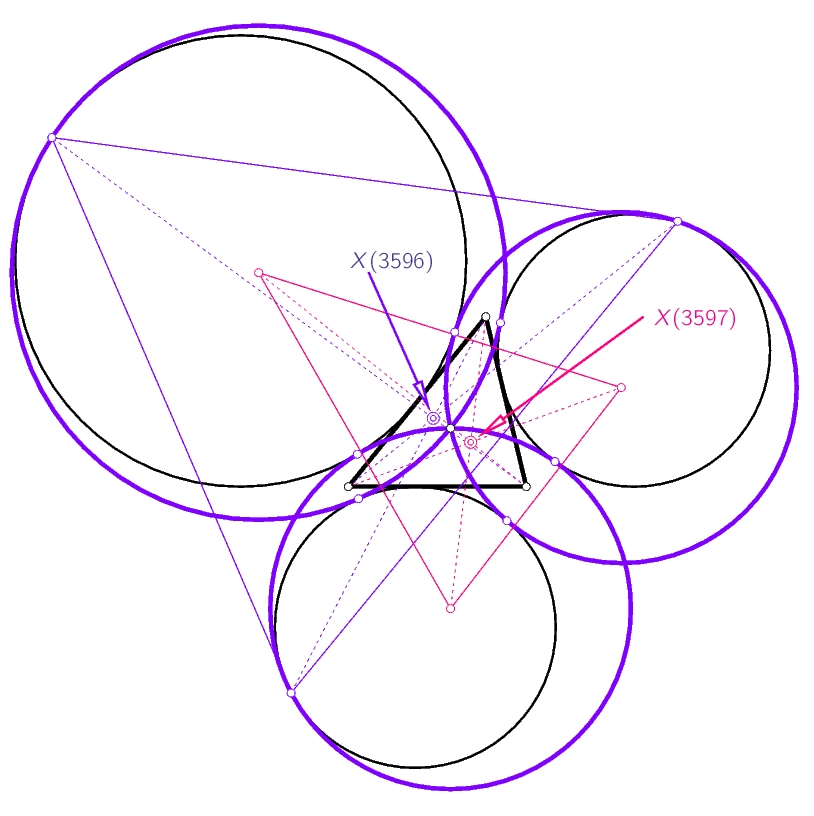
circles tangent to We study those tritangent circles of the excirlces of a triangle which enclose exactly one excircle and touch the two others from the outside. It turns out that these three circles share exactly the Spieker point. Moreover we show that these circles give rise to some triangles which are in perspective with the base triangle. The respective perspectors turn out to be new polynomial triangle centers. |
Publications
|